“Statistisch signifikant”, das hört oder liest man ziemlich schnell mal, wenn es irgendwie um Wissenschaft und Daten geht. Der Ausdruck soll darauf hindeuten, dass irgendein Zusammenhang oder Effekt bedeutsam oder real ist. Tatsächlich ist die Idee von statistischer Signifikanz nicht mehr aus wissenschaftlicher Forschung wegzudenken. Das ist nicht ganz unproblematisch: In Tat und Wahrheit ist statistische Signifikanz ein ziemlich wirres Konzept, das praktisch für viele Probleme sorgt.
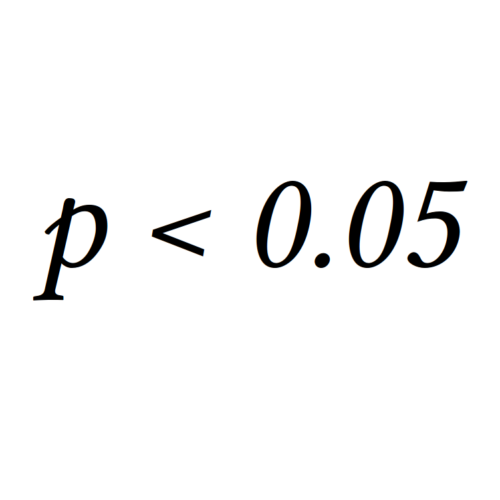
Oft misinterpretiert und doch so zentral in der Wissenschaft: Der p-Wert unter der „signifikanten“ 0.05-Grenze.
Weiterführende Links
- Gastbeitrag von Co-Host Marko Kovic in der NZZ: Fallstricke der Statistik – Die Wissenschaft in der Replikationskrise
- A Dirty Dozen: Twelve P-Value Misconceptions
- P Values and Statistical Practice
- The fallacy of the null-hypothesis significance test
- The statistical crisis in science
- The ASA’s Statement on p-Values: Context, Process, and Purpose
- The fallacy of placing confidence in confidence intervals
- Eine frühere Folge von skeptisCH mit verwandtem Inhalt: skeptisCH – Folge 44: Wahrscheinlichkeiten
—
Den Podcast abonnieren:
Im Podcast verwendete Musik:

8 Comments on “skeptisCH – Folge 54: Statistisch signifikant”
Pingback: Psiram » Psirama – Der Psiram-Wochenrückblick (KW21, 2017)
Der p-Wert ist NICHT „die Wahrscheinlichkeit der beobachteten Daten wenn wir glauben, dass das Nullmodell wahr ist“ (Minute 5).
Der p-Wert berechnet die Wahrscheinlichkeit des Ergebnisses eines Zufallsexperiments (unter Annahme des Nullmodells), das mindestens so extrem ist wie das Ergebnis unserer tatsächlichen Beobachtung.
Hallo xnor
Also, würdest du sagen dass p-Werte eher etwas mit
1) Pr(null | data)
oder eher etwas mit
2) Pr(data | null)
zu tun haben?
Wenn du 2) glaubst, dann glauben wir dasselbe. Und, für die Mitlesenden: Schwammige Ausdrücke wie „unter der Annahme“ etc. bedeutet eben schlicht, dass wir glauben, dass das Nullmodell wahr ist (im Alltagsdeutsch hat der Begriff Glaube eine leicht andere Konnotation als das Englische Belief – es geht aber in beiden Fällen in diesem Kontext um eine simple erkenntnistheoretische Konstellation).
Im Podcast erwähnen wir, glaube ich, nur ein Mal explizit, dass es um dieselben und noch extremere Daten geht; danach sprechen wir pars pro toto von Daten. Ich hoffe, das ist nicht verwirrend.
Die ganz genaue technische Definition von p-Werten ist nicht so wichtig; es geht um die Wahrscheinlichkeit bestimter Teststatistiken. Geht in diese Richtung:
Pr(T(yrep) > T(y)|null)
Der erkenntnistheoretische Knackpunkt von p-Werten ist die Logik von 1) vs. 2).
Grüsse
Hey Marko,
natürlich 2, denn 1 wäre ja komplett falsch (und das ist auch der Irrglaube, der im Podcast richtigerweise „angeprangert“ wird.)
„Unter der Annahme“ finde ich nicht schwammig. Wir nehmen ja an, dass das Nullmodell wahr ist, und unter dieser Annahme berechnen wir die Wahrscheinlichkeit, dass das Ergebnis eines entsprechenden Zufallsexperiments mindestens so extrem wie unser tatsächlich gemessenes Ergebnis ist.
Problematischer finde ich dass gesagt wird, dass wir die Wahrscheinlichkeit der Daten berechnen.
Vielleicht wäre ein kleines Beispiel hilfreich:
In einem Test werden einer Person zB zwei Referenzstücke A und B gezeigt. In 10 Runden wird eines der beiden zufällig ausgewählt und die Person muss sagen, ob es sich dabei um A oder B handelt.
Es liegt eine Binomialverteilung vor. Aus dem Experiment wissen wir N=10.
Im Nullmodell nehmen wir an, dass die Person bloße Raterei betreibt.
Durch diese Annahme fixieren wir die Wahrscheinlichkeit des Erfolgs in einer Runde auf p=0,5!
P(8 oder mehr richtige | bloße Raterei) = 0,055
P(9 richtige | bloße Raterei) = 0,01
P(10 richtige | bloße Raterei) = 0,001
Wir berechnen also nicht die Wahrscheinlichkeit des Testergebnisses (der Daten), sondern wie wahrscheinlich es ist, dass durch Zufall mindestens so gut geraten wird.
Das Signifikanzniveau (zB 5%) gibt somit eigentlich an, wie tolerant man gegenüber falschem Verwerfen eines tatsächlich wahren Nullmodells ist.
Wenn wir 1000 Personen den Test absolvieren lassen, die aber alle nur raten, dann erhalten wir rein statistisch ~50 Testergebnisse mit p-Wert < 5%.
Merci für die Replik!
Ich glaube nicht, dass wir die Situation sehr anders einschätzen – aber ich glaube auch nicht, dass wir uns einiger werden, als wir es jetzt sind :).
Ad „Annahme“, „Vermutung“, usf.: Solche doxastischen Einstellungen („doxastic attitudes“; weiss nicht, ob der Begriff so auch zu Deutsch gebraucht wird!) sind insofern ungenauer und unpräziser als der Ausdruck „Glaube“, weil die meisten Leute nicht realisieren, was es mit doxastischen Einstellungen überhaupt auf sich hat. Das ist auch der Grund, warum ich z.B. von „Nullmodell“ anstatt „Nullhypothese“ spreche – „Modell“ impliziert, dass wir einen recht starken und recht genauen Glauben über die Realität kundtun, während „Hypothese“ nach „könnte ja sein; ist einfach eine Idee“ tönt.
Dass es bei p-Werten um hypothetical frequentism geht (imaginierte unendlich oft wiederholte Datengenerierung) erklären wir ziemlich explizit im Podcast, glaube ich; hier sollte es für die Zuhörenden keine Verwirrung geben. Vielleicht hätten wir uns aber wirklich etwas anders ausdrücken sollen; z.B. „Wahrscheinlichkeit für solche oder noch extremere Daten gegeben des Nullmodells“.
„Das Signifikanzniveau (zB 5%) gibt somit eigentlich an, wie tolerant man gegenüber falschem Verwerfen eines tatsächlich wahren Nullmodells ist.“
Solche Metaphern wiederum gefallen mir überhaupt nicht, weil sie sehr ungenau und unpräzise sind (z.B. ist komplett unklar, was „tolerant“ für eine doxastische Einstellung sein soll…). Die Probleme mit NHST sind logisch und erkenntnistheoretisch verschachtelter als bloss mit p-Werten und gehen weiter, als wir im Podcast diskutieren (ich glaube z.B. nicht, dass es, rationalerweise, in den allermeisten Kontexten so etwas wie Typ I- und II-Fehler gibt, weil es so gut wie nie „wahre“ Nullmodelle gibt; begegnet sind mir in der Realität jedenfalls noch keine).
Die Kernbotschaft im Podcast stützt du aber sicher auch:
– Signifikanzniveaus sind willkürliche Konventionen.
– Diese willkürlichen Konventionen haben sehr grosse praktische Probleme („Signifikanzfilter“ bei Journals, p-Hacking, etc.).
Gruss
„Annahme“, „Nullhypothese“ (was auch nichts weiteres ist als eine Annahme) sind eigentlich klare Ausdrücke, die zumindest in meiner Verwendung nichts über Glauben oder die Realität aussagen.
Wenn ich x=10 in einer Gleichung annehme (also für x 10 einsetze und weiter rechne), dann sage ich auch nichts über meinen Glauben oder die Realität aus.
Die Kritik über den Satz über das Signifikanzniveau ist vollkommen berechtigt. Ich hätte nicht „tatsächlich wahr“ sondern „als wahr angenommenes“ schreiben sollen.
Dieser Widerspruch (wir nehmen die NH an, aber verwerfen sie zB in 5% der Fälle) wurde ja auch im Podcast angesprochen.
Natürlich hast du recht, dass es grobe Probleme damit gibt, wenn man damit Schlüsse über die Realität ziehen möchte.
Ganz richtig auch, dass es so eine „Punkt“-Nullhypothese in der Praxis gar nicht gibt. Dazu auch folgende interessante Überlegung:
Wenn wir N in meinem vorherigen Beispiel gegen Unendlich gehen lassen, dann geht (mindestens notwendige richtige)/N gegen 50% .. um die NH zu verwerfen.
Die frequentistische Statistik hatte einfach mehr Zeit zur Verfügung gehabt, um missbraucht zu werden. In 50 Jahren sprechen wir vielleicht nicht mehr von p-Hacking sondern von apriori-Schlammschlachten.
Das kann gut sein! 🙂
Im bayesianischen Lager gibt es z.B. schon jetzt die Schule der „Bayes Factor“-Verfechter, um Hypothesentests zu machen – und ich glaube, dass der Einsatz von Bayes Factors *mindestens* so problematisch ist wie frequentistische NHST.